Bradley University Topology Class

Monthly Archives: March 2015

Getting some terms straight: limit points, accumulation points, etc.

Leave a comment Posted by collegemathteaching on March 31, 2015

Homework (due April 8): Mendelson, 5.4, 1, 2, 3 (pages 171-172) 5.5 1, 2, 3, 4, 5 (page 178).

We will be talking about compactness and its consequences in metric spaces. So we will be using many similar but logically distinct concepts, so I thought I’d present a guide.
The setting: $X$ will be topological space with a topology $\mathscr{T}$ , $A \subset X$ and $x \in X$ .

1. Limit point. We say that $x \ X$ is a limit point for $A$ if every open set $U$ containing $x$ contains a point of $A$ other than $x$ .
Put another way: $x$ is a limit point for $A$ is for every open $U, x \in U$ we have $(U -\{x \}) \cap A \neq \emptyset$ .

Note: sometimes $U- \{x \}$ is called a deleted open neighborhood of $x$ .

Note: $x$ need not be in $A$ .

Note: there is no requirement regarding the cardinality of $(U - \{ x \} ) \cap A$ ; the intersection just has to be nonempty.

Example: consider the 4 point set $\{ 1, 2, 3, 4 \}$ with the topology being: $\emptyset, \{ 1, 2, 3, 4 \}, \{1, 2, 3 \}, \{4 \}$ . Then if $A = \{1, 2 \}$ , the point $3$ is a limit point for $A$ . The point 4 is not.

2. Accumulation point (sometimes called cluster point, especially in the context of nets). A point $x$ is an accumulation point for $A$ if for every open $U, x \in U, |U \cap A |$ is infinite. An accumulation point is a limit point but not all limit points are accumulation points; see the finite topology example in part 1.

Example: in the usual topology, $0$ is an accumulation point for $(0,1)$ as well as for the sequence $\{1, \frac{1}{2}, \frac{1}{3}, ......\frac{1}{n}, ....\}$ .

3. Condensation point. We say that $x$ is a condensation point of a set $A$ if for every open set $U, x \in U, |U \cap A |$ is uncountable. In the previous example: $0$ is a condensation point for $(0,1)$ but not for the sequence $\{1, \frac{1}{2}, \frac{1}{3}, ......\frac{1}{n}, ....\}$ . In fact, no sequence can have a condensation point (why?) but a net can.

4. (advanced) Perfect Limit Point We say that $x$ is a perfect limit point for $A$ if for all $U, x \in U$ we have $|A \cap U| = |A|$ . That is, any open neighborhood of $x$ contains “as many” points of $A$ as $A$ has. If this seems strange, remember that infinite cardinals behave in non-intuitive ways. Example: $(0,1)$ has as many points as $R^1$ does. In fact, a bijection between these two sets is given by $f(x) = \frac{x - \frac{1}{2}}{x(1-x)}$ (in fact this is a homeomorphism) between $(0,1)$ and $R$ .

Example: $0$ is a perfect limit point for both $(0,1)$ and for $\{1, \frac{1}{2}, \frac{1}{3}, ....\frac{1}{n}..... \}$ .

Here is an example of a limit point that is not perfect: consider $B =(-1,0) \cup \{\frac{1}{2}, \frac{2}{3}, \frac{3}{4}, ...\frac{n-1}{n}....\}$ . The points $0$ and $-1$ (and any $x, -1 < x < 0$ ) are perfect limit points; 1 is a limit point but not a perfect limit point. Remember that $|B|$ is uncountable.

Sequences
Remember that a sequence is a map $f: \{1, 2, 3,... \} \rightarrow X$ where $f(n)$ is often denoted by $a_n$ . Now a sequence $a_n$ is said to converge to $a$ if for any open set $U$ containing $a$ there is some positive integer $M$ such that, for all $n > M, a_n \in U$ . That is, $U$ contains an entire “tail” of the sequence $a_n, a_{n+1}, .....$ . Sometimes this is stated that $a_n$ is eventually in $U$ .

Side note: if $b$ is any accumulation point of the sequence, and $V$ is any open set containing $b$ then we say that $a_n$ is frequently in $V$ .

Summary: “eventually” in $V$ means that $V$ contains an entire tail of the sequence; “frequently” means that $V$ contains an infinite number of points of the sequence, but possibly not an entire tail.

So if the sequence converges to $a$ then $a$ is said to be a limit of the sequence. Note that the limit of a sequence (if it has one) is a limit point of the sequence (actually, a limit point of the image of the sequence, but we are rarely that pedantic) and, in fact, an accumulation point of the sequence.

Note that a sequence can have more than one accumulation point (e. g. $\frac{1}{2}, \frac{1}{3}, \frac{2}{3}, \frac{1}{4}, \frac{3}{4}, .....\frac{1}{n}, \frac{n-1}{n}, ...$ and IN A HAUSDORFF SPACE, this means that the sequence has no limit.

Exercise: give $R^1$ the finite complement topology. Then if $a_n$ is any sequence which attains an infinite number of distinct values, $a_n \rightarrow x$ for ANY $x \in R^1$ . This shows that whether a sequence converges or not depends not only on the sequence itself but also on the topology in question.

Worksheet for the finite product Tychonoff Theorem.

Leave a comment Posted by collegemathteaching on March 30, 2015

Let $X \times Y$ be the product of two compact spaces $X$ and $Y$ . We want to show that $X \times Y$ is compact. Let $\mathscr{U}$ be an open cover of $X \times Y$ ; we can assume that each open set in this cover is of the form $U_{\beta} \times V_{\beta}$ where $U_{\beta}, V_{\beta}$ are open sets in $X, Y$ respectively (remember that the box and product topologies are equivalent when the product is finite).

To understand this theorem, prove each of the following:

1. Let $x \in X$ . Then $\{x \} \times Y$ is homeomorphic to $Y$ . (the homeomorphism is $f(y) = (x, y) \in X \times Y$

2. $\{x \} \times Y$ is a compact subset of $X \times Y$ .

3. A finite subcollection of $\mathscr{U}$ covers $\{x \} \times Y$ ; call this $\cup^{k_x}_{i=1} U_{i,x} \times V_{i,x}$ . The $x$ in the subscript and in the number of open sets indicates that this open subcover is associated with $\{x \} \times Y$ .

4. $\cap^{k_x}_{i=1}U_{i,x}$ is an open set in $X$ which contains $x$ .

5. The open set $U_{i,x} \times Y$ is a subset of the open set $\cup^{k_x}_{i=1} U_{i,x} \times V_{i,x}$ . We say that the latter open set is the “part of the open cover” associated with $U_{i,x}. 6. Do this procedure for each$ latex x \in X $. Then if $U_x = \cap^{k_x}_{i=1}U_{i,x}$ , then $\cup_{x \in X}U_x$ is an open cover for $X$ . Therefore there is a finite subcover $U_{x_i}, i \in \{1, ...m \}$ which covers $X$ .

7. Then the collection $U_{x_i} \times Y, i \in \{1, ...,m \}$ covers all of $X \times Y$ . (show that if $(x,y) \in X \times Y$ then $(x,y)$ lies in at least one of these open sets.

8. The desired “finite open subcover of $X \times Y$ is the collection of associated finite subcovers discussed in 5.

compact spaces product topology, Tychonoff Theoream, Tychonoff worksheet

Assorted results related to compact spaces and compact subsets

Leave a comment Posted by collegemathteaching on March 29, 2015

1. Let $X$ be a compact topological space and let $C$ be a closed subset of $X$ . Then $C$ is compact.

Proof. Let $\mathscr{O}$ be an open cover for $C$ . Then $(X - C ) \cup ( \cup_{O \in \mathscr{O} } )$ is an open cover of $X$ and therefore has a finite subcover $(X-C) \cup ( \cup^k_{i=1} O_i )$ where each $O_i \in \mathscr{O}$ . Note that $(X-C) \cup ( \cup^k_{i=1} O_i )$ is an open cover for $C$ and that $(X-C) \cap C = \emptyset$ . Therefore $\cup^k_{i=1} O_i$ covers $C$ and is the required finite open subcover.

2. If $X$ is a Hausdorff topological space and $C \subset X$ is compact, then $C$ is closed.

Proof. We show that if $y \in X -C$ , then there is an open set $U$ where $y \in U \subset X -C$ which shows that $X-C$ is open.

For each $c \in C$ find disjoint open sets $U_c, V_c$ where $y \in U_c, c \in V_c$ . Cover $C$ by $U_{c \in C} V_c$ . Now $\cap_{c \in C} U_c$ contains $c$ BUT MIGHT NOT BE OPEN as the intersection might be an infinite one. But that is ok; because $C$ is compact there are a finite collection of the $V_c$ that cover; say $\cup^k_{i=1} V_{ci}$ . Then $y \in \cap^k_{i=1} U_{ci}$ which is an open set which is disjoint from $\cup^k_{i=1} V_{ci}$ and therefore disjoint from $C$ .

Note: That $X$ is Hausdorff is essential. Consider $R^1$ in the finite complement topology. Then $R - {1}$ is not a closed subset but is compact. For if we have any open cover, let $U$ be any element of the open cover. $R - U$ is a finite set $\{ a_1, a_2, ..a_k \}$ and for each $a_i \neq 1$ choose and open set from the cover that contains that $a_i$ , and we can do this with a finite number of open sets.

3. A compact Hausdorff space is regular ( $T_3$ ).

Proof. If $C$ is a closed set in a compact space, $C$ is compact. So if $y \in X-C$ , the construction in proof 2 can be used without modification to find disjoint open sets; one containing $y$ and the other containing $C$ .

4. Limit point compactness for compact spaces: if $X$ is a compact topological space and $A \subset X$ is an infinite set, then $A$ has a limit point. Note: compactness is necessary; for example $Z \subset R^1$ (usual topology) is an infinite set without a limit point.

Proof. We show the following: if $A \subset X$ is a set without limit points, then $A$ is finite.
Now if $A$ has no limit points, $A$ is closed. Since $X$ is compact, so is $A$ (closed subset of a compact space). Since $A$ has no limit points, for each $a \in A$ there is an open set $U_a$ (open in $X$ that contains exactly one point of $A$ , namely $a$ . $\cup_{a \in A} U_a$ is an open cover which must have a finite subcover $\cup^k_{i=1}U_{ai}$ . But each of these open sets contains exactly one point of $A$ and covers $A$ , hence $A$ must be finite.

Since all subsets of compact spaces that have no limit points are finite sets, any infinite subset must have a limit point.

5. Finite intersection property: let $X$ be a compact topological space and let $\mathscr{C}$ be any collection of closed sets. If $\cap_{C \in \mathscr{C} } C = \emptyset$ then there is a finite subcollection of $\mathscr{C}$ such that $\cap^k_{i=1} C_i = \emptyset$ .

Note: this is an important result used in real analysis, complex variables and in differential equations, sometimes under the guise of “nested closed intervals” or “nested rectangles”. Compactness and closed sets is essential; after all $\cap_{n=1}^{\infty} (0, \frac{1}{n}) = \emptyset$ though the intersection of any finite subcollection of these sets is non-empty.

Proof. Try this yourself before looking!

Suppose $\cap_{C \in \mathscr{C} } C = \emptyset$ . Then $X - \cap_{C \in \mathscr{C} } C = X$ and $X - \cap_{C \in \mathscr{C} } C = \cup_{C \in \mathscr{C} } (X - C)$ (by DeMorgan’s laws) which is an open cover of $X$ which is compact. Hence a finite subcover will suffice: $\cup_{i=1}^k (X - C_i) = X- \cap_{i=1}^k C_i = X$ which implies that $\cap_{i=1}C_i = \emptyset$ . Remember that each $C_i \in \mathscr{C}$ . This is the finite subcollection that has empty intersection.

6. Finally, a result that I use all of the time.

Let $X$ be compact, $Y$ be Hasudorff and $f: X \rightarrow Y$ a continuous bijection which is onto. Then $f$ is a homeomorphism.

Proof. Since $f$ is onto and continuous and $X$ is compact, so is $Y$ . Now let $C \subset X$ be closed. $f(C)$ is compact in $Y$ (continuous image of a compact set is compact) and because $Y$ is Hausdorff, $f(C)$ is closed. So for $C \subset X$ closed, $(f^{-1})^{-1} (C) = f(C)$ is closed, hence the inverse function is also continuous. Hence $f$ is a homeomorphism (continuous, bijection, continuous inverse).

Note: the hypothesis are all necessary. For example, consider $f:([0,1], \mathscr{T}_1) \rightarrow ([0,1], \mathscr{T}_2 )$ where $f(x) = x$ and $\mathscr{T}_1$ is the discrete topology and $\mathscr{T}_2$ is the usual (subspace) topology. $f$ is a continuous bijection and the image space is Hausdorff but $f$ is NOT a homeomorphism.

Hausdorff is essential as well; consider the identity map (above) but now let $\mathscr{T}_1$ be the usual subspace topology for $[0,1]$ and $\mathscr{T}_2$ be the finite complement topology. Of course since finite sets are closed in the usual topology, the finite complement topology is coarser than the usual topology. Hence $f(x) = x$ is continuous and $[0,1]$ is compact (as is the image space!). But $f$ is not a homeomorphism as the image space is not Hausdorff.

compact spaces, continuous functions, functions, homeomorphism, Separation Axioms, topologies properties of compact spaces

Tychonoff Theorem: finite product of compact spaces is compact

Leave a comment Posted by collegemathteaching on March 27, 2015

Ok, now lets prove the following: If $X, Y$ are compact spaces, then $X \times Y$ is compact (in the usual product topology). Note: this effectively proves that the finite product of compact spaces is compact. One might call this a “junior” Tychonoff Theorem.

Proof. We will prove this theorem a couple of times; the first proof is the more elementary but less elegant proof. It can NOT be easily extended to show that the arbitrary product of compact spaces is compact (which is the full Tychonoff Theorem).

We will show that an open covering of $X \times Y$ by basis elements of the form $U \times V$ , $U$ open in $X$ and $V$ open in $Y$ has a finite subcover.

So let $\mathscr{U}$ be an open cover of $X \times Y$ . Now fix $x_{\beta} \in X$ and consider the subset $x_{\beta} \times Y$ . This subset is homeomorphic to $Y$ and is therefore compact; therefore there is a finite subcollection of $\mathscr{U}$ which overs $x_{\beta} \times Y$ , say $\cup^{\beta, k}_{i=1} U_{\beta, i} \times V_{\beta, i}$ Note that each $U_{\beta, i}$ is an open set in $X$ which contains $x_{\beta}$ and there are only a finite number of these. Hence $\cap^{\beta k}_{i=1} U_{\beta i} = U_{\beta}$ is also an open set which contains $x_{\beta}$ . Also know that $U_{\beta} \times Y \subset \cup^{\beta, k}_{i=1} U_{\beta, i} \times V_{\beta, i}$

We can do this for each $x_{\beta} \in X$ and so obtain an open cover of $X$ by $\cup_{x_{\beta} \in X} U_{\beta}$ and because $X$ is compact, a finite subcollection of these covers $X$ . Call these $U_1, U_2, U_3....U_m$ . For each one of these, we have $U_j \times Y \subset \cup^{j, k}_{i=1} U_{j, i} \times V_{j, i}$ .

So, our finite subcover of $X \times Y$ is $\cup^m_{j=1}\cup^{j, k}_{i=1} U_{j, i} \times V_{j, i}$ .

Now while this proof is elementary, it doesn’t extend to the arbitrary infinite product case.

So, to set up such an extension, we’ll give some “equivalent” definitions of compactness. Note: at some point, we’ll use some elementary cardinal arithmetic.

compact spaces Tychonoff Theorem

Compact Spaces: terse introduction

Leave a comment Posted by collegemathteaching on March 23, 2015

Note to the class: these are notes I wrote for my math blog; the pace might be a bit quick for a first go-around. We’ll discuss these ideas over a few class periods, and I might put some more material.

Exercises for 27 March: Mendelson: 5.2: 1, 2, 4, 5, 5.3: 2, 3, 4.

So, what do we mean by “compact”?

Instead of just blurting out the definition and equivalent formulations, I’ll try to give some intuition. If we are talking about a subset of a metric space, a compact subset is one that is both closed and bounded. Now that is NOT the definition of compactness, though it is true that:

Given a set $X \subset R^n$ , $X$ is compact if and only if $X$ is both closed (as a topological subset) and bounded (in that it fits within a sufficiently large closed ball). In $R^1$ compact subsets can be thought of as selected finite unions and arbitrary intersections of closed intervals. In the higher dimensions, think of the finite union and arbitrary intersections of things like closed balls.

Now it is true that if $f:X \rightarrow Y$ is continuous, then if $X$ is a compact topological space, then $f(X)$ is compact (either as a space, or in the subspace topology, if $f$ is not onto.

This leads to a big theorem of calculus: the Extreme Value Theorem: if $f:R^n \rightarrow R$ is continuous over a compact subset $D \subset R^n$ then $f$ attains both a maximum and a minimum value over $D$ .

Now in calculus, we rarely use the word “compact” but instead say something about $D$ be a closed, bounded subset. In the case where $n = 1$ we usually say that $D =[a,b]$ , a closed interval.

So, in terms of intuition, if one is thinking about subsets of $R^n$ , one can think of a compact space as a domain on which any continuous real valued function always attains both a minimum and a maximum value.

Now for the definition
We need some terminology: a collection of open sets $U_{\alpha}$ is said to be an open cover of a space $X$ if $\cup_{\beta \in I } U_{\beta} = X$ and if $A \subset X$ a collection of open sets is said to be an open cover of $A$ if $A \subset \cup_{\beta \in I } U_{\beta}$ A finite subcover is a finite subcollection of the open sets such that $\cup^k_{i=1} U_i = \cup_{\beta \in I} U_{\beta}$ .

Here is an example: $(\frac{3}{4}, 1] \cup^{\infty}_{n=1} [0, \frac{n}{n+1})$ is an open cover of $[0,1]$ in the subspace topology. A finite subcover (from this collection) would be $[0, \frac{4}{5}) \cup (\frac{3}{4}, 1]$

Let $X$ be a topological space. We say that $X$ is a compact topological space if any open over of $X$ has a finite subcover. If $C \subset X$ we say that $C$ is a compact subset of $X$ if any open cover of $C$ has a finite subcover.

Prior to going through examples, I think that it is wise to mention something. One logically equivalent definition is this: A space (or a subset) is compact if every cover by open basis elements has a finite subcover. Here is why: if $X$ is compact, then ANY open cover has a finite subcover, and an open cover by basis elements is an open cover. On the other hand: if we assume the “every open cover by open basis elements has a finite subcover” condition: then if $\mathscr{U}$ is an open cover, then we can view this open cover as an open cover of the basis elements whose union is each open $U_{\beta} \in \mathscr{U}$ . This open cover of basis elements has a finite subcover of basis elements..say $B_1, B_2, ....B_k$ . Then for each basis element, choose a single $U_i \in \mathscr{U}$ for which $B_i \subset U_i$ . That is the required open subcover.

Now, when convenient, we can assume that the open cover in question (during a proof) consists of basic open sets. That will simplify things at times.

So, what are some compact spaces and sets, and what are some basic facts?

Let’s see some compact sets, some non compact sets and see some basic facts.

1. Let $X$ be any topological space and $A \subset X$ a finite subset. Then $A$ is a compact subset. Proof: given any open cover of $A$ choose one open set per element of $A$ which contains said element.

2. Let $R$ have the usual topology. Then the integers $Z \subset R^1$ is not a compact subset; choose the open cover $\cup^{\infty}_{n = -\infty} (n - \frac{1}{4}, n+ \frac{1}{4})$ is an infinite cover with no finite subcover. In fact, ANY unbounded subset $A \subset R^n$ in the usual metric topology fails to be compact: for $a \in A$ with $d(a, 0) \geq n$ choose $B_a(\frac{1}{n})$ ; clearly this open cover can have no finite subcover.

3. The finite union of compact subsets is compact (easy exercise).

4. If $C \subset X$ is compact and $X$ is a Hausdorff topological space ( $T_2$ ) then $C$ is closed. Here is why: let $x \notin C$ and for every $c \in C$ choose $U_c, V_c$ open where $x \in U_c, c \in V_c$ . Now $\cup_{c \in C}V_c$ is an open set which contains $C$ and has a finite subcover $\cup_{i=1}^k V_i$ Note that each $U_i$ is an open set which contains $x$ and now we have only a finite number of these. Hence $x \in \cap^k_{i=1} U_i$ which is disjoint from $\cup_{i=1}^k V_i$ which contains $C$ . Because $x$ was an arbitrary point in $X -C$ , $X-C$ is open which means that $C$ is closed. Note: this proof, with one minor addition, shows that a compact Hausdorff space is regular ( $T_3$ ) we need only show that a closed subset of a compact Hausdorff space is compact. That is easy enough to do: let $\mathscr{U}$ be an open cover for $C$ ; then the collection $\mathscr{U} \cup (X-C)$ is an open cover for $X$ , which has a finite subcover. Let that be $\cup^k_{i=1} U_i \cup (X-C)$ where each $U_i \in \mathscr{U}$ . Now since $X-C$ does not cover $C, \cup^k_{i=1} U_i$ does.

So we have proved that a closed subset of a compact set is compact.

5. Let $R$ (or any infinite set) be given the finite complement topology (that is, the open sets are the empty set together with sets whose complements consist of a finite number of points). Then ANY subset is compact! Here is why: let $C$ be any set and let $\mathscr{U}$ be any open cover. Choose $U_1 \in \mathscr{U}$ . Since $X -U_1$ is a finite set of points, only a finite number of them can be in $C$ , say $c_1, c_2, ...c_k$ . Then for each of these, select one open set in the open cover that contains the point; that is the finite subcover.

Note: this shows that non-closed sets can be compact sets, if the underlying topology is not Hausdorff.

6. If $f: X \rightarrow Y$ is continuous and onto and $X$ is compact, then so is $Y$ . Proof: let $\cup_{\beta \in I} U_{\beta}$ cover $Y$ and note that $\cup_{\beta}f^{-1}(U_{\beta})$ covers $X$ , hence a finite number of these open sets cover: $X = \cup^{k}_{i=1}f^{-1}(U_i)$ . Therefore $\cup^k_{i=1}U_i$ covers $Y$ . Note: this shows that being compact is a topological invariant; that is, if two spaces are homeomorphic, then either both spaces are compact or neither one is.

7. Ok, let’s finally prove something. Let $R^1$ have the usual topology. Then $[0, 1]$ (and therefore any closed interval) is compact. This is (part) of the famous Heine-Borel Theorem. The proof uses the least upper bound axiom of the real numbers.

Let $\mathscr{U}$ be any open cover for $[0,1]$ . If no finite subcover exists, let $x$ be the least upper bound of the subset $F$ of $[0,1]$ that CAN be covered by a finite subcollection of $\mathscr{U}$ . Now $x > 0$ because at least one element of $\mathscr{U}$ contains $0$ and therefore contains $[0, \delta )$ for some $\delta > 0$ . Assume that $x < 1$ . Now suppose $x \in F$ , that is $x$ is part of the subset that can be covered by a finite subcover. Then because $x \in U_{\beta}$ for some $U_{\beta} \in \mathscr{U}$ then $(x-\delta, x + \delta) \subset U_{\beta}$ which means that $x + \delta \in F$ , which means that $x$ isn’t an upper bound for $F$ .

Now suppose $x \notin F$ ; then because $x < 1$ there is still some $U_{\beta}$ where $(x-\delta, x+ \delta) \subset U_{\beta}$ . But since $x = lub(F)$ then $x - \delta \in F$ and so $[0, x- \delta ) \subset F$ . So if $F$ can be covered by $\cup^k_{i=1} U_i$ then $\cup^k_{i=1} U_i \cup U_{\beta}$ is a finite subcover of $[0, x + \delta )$ which means that $x$ was not an upper bound. It follows that $x = 1$ which means that the unit interval is compact.

Now what about the closed ball in $R^n$ ? The traditional way is to show that the closed ball is a closed subset of a closed hypercube in $R^n$ and so if we show that the product of compact spaces is compact, we would be done. That is for later.

8. Now endow $R^1$ with the lower limit topology. That is, the open sets are generated by basis elements $[a, b)$ . Note that the lower limit topology is strictly finer than the usual topology. Now in this topology: $[0,1]$ is not compact. (note: none of $(0,1), [0,1), (0, 1]$ are compact in the coarser usual topology, so there is no need to consider these). To see this, cover $[0,1]$ by $\cup ^{\infty}_{n=1} [0, \frac{n}{n+1}) \cup [1, \frac{3}{2})$ and it is easy to see that this open cover has no finite subcover. In fact, with a bit of work, one can show that every compact subset is at most countable and nowhere dense; in fact, if $A$ is compact in the lower limit topology and $a \in A$ there exists some $y_a$ where $(y_a, a) \cap A = \emptyset$ .

compact spaces compact spaces, compact subsets

Radial Topology: interesting example

Leave a comment Posted by collegemathteaching on March 13, 2015

Willard (in the book General Topology) defines something called the “radial plane”: the set of points is $R^2$ and a set $U$ is declared open if it meets the following property: for all $\vec{x} \in U$ and each unit vector $\vec{u}_{\theta} = \langle cos(\theta), sin(\theta) \rangle$ there is some $\epsilon_{\theta} > 0$ such that $\vec{x} + \epsilon_{\theta} \vec{u}_{\theta} \subset U$

In words: a set is open if, for every point in the set, there is an open line segment in every direction from the point that stays with in the set; note the line segments do NOT have to be of the same length in every direction.

Of course, a set that is open in the usual topology for $R^2$ is open in the radial topology.

It turns out that the radial topology is strictly finer than the usual topology.

~~I am not going to prove that here~~ but I am going to show a very curious closed set.

Consider the following set $C = \{(x, x^4), x > 0 \}$ . In the usual topology, this set is neither closed (it lacks the limit point $(0,0)$ ) nor open. But in the radial topology, $C$ is a closed set.

To see this we need only show that there is an open set $U$ that misses $C$ and contains the origin (it is easy to find an open set that shields other points in the complement from $C$ . )

First note that the line $x = 0$ contains $(0,0)$ and is disjoint from $C$ , as is the line $y = 0$ . Now what about the line $y = mx$ ? $mx = x^4 \rightarrow x^4-mx = (x^3-m)x = 0$ and so the set $\{(x, mx) \}$ meets $C$ only at $x = m^{\frac{1}{3}}, y = m^{\frac{4}{3}}$ and at no other points; hence, by definition, $R^2 - C$ is an open set which contains $(0,0)$ .

Of course, we can do that at ANY point on the usual graph of $f(x) = x^4$ ; the graphs of such “curvy” functions have no limit points.

Therefore such a graph, in the subspace topology…has the discrete topology.

On the other hand, the lattice of rational points in the plane form a countable, dense set (a line segment from a rational lattice point with a rational slope will intercept another rational lattice point).

So we have a separable topological space that lacks a countable basis: $R^2$ with the radial topology is not metric. Therefore it is strictly finer than the usual topology.

PS: I haven’t checked the above carefully, but I am reasonably sure it is right; a reader who spots an error is encouraged to point it out in the comments. I’ll have to think about this a bit.

metric spaces, topologies non-metrizable space, radial plane topology

Regularity and Normality

Leave a comment Posted by collegemathteaching on March 9, 2015

We start with the assumption of $T_1$ : that one point sets are closed. That will be our operating assumption throughout.

We call a topological space “regular” ( $T_3$ ) if the following holds: given $x$ and closed set $C, x \notin C$ , there exists open sets $U, V$ where $x \in U, C \subset V$ and $U \cap V = \emptyset$ .

Theorem: $X$ is a regular topological space if and only if the following condition (I) holds: let $x \in U$ open. Then there exists an open set $V$ where $x \in V$ and $\bar{V} \subset U$ .

Proof. Let $X$ be regular. Let $x \in U$ where $U$ is open. Then $x \notin X - U$ so there exists open $V, W$ where $x \in V, (X-U) \subset W$ and $V \cap W = \emptyset$ . Claim: $\bar{V} \subset U$ . Clearly $V \subset U$ because $X - U \subset W$ . No point of $W$ can be a limit point of $V$ since $W \cap V = \emptyset$ . So $\bar{V} \subset U$ as required.

Now let $X$ meet condition I. If $x \in X-C$ , then there exists open $V$ where $x \in V$ and $\bar{V} \subset X-C$ . Now find $W$ open where $x \in W, \bar{W} \subset V$ . Then the disjoint open sets are $W, X - V$ where $x \in W, C \subset X-V$ .

Theorem (homework): metric spaces are regular.

Proof: one point sets are closed (metric spaces are Hausdorff, therefore $T_1$ . So we can meet condition 1 as follows: if $U$ is an open set containing $x$ , then there is some $\delta > 0$ where $B_x(\delta) \subset U$ . Let $V = B_x(\frac{\delta}{2})$ and then $\bar{V} \subset U$ . So metric spaces meet condition I and are therefore regular.

Normal Spaces A space is normal ( $T_4$ ) if, given two closed sets $C, D$ where $C \cap D = \emptyset$ there exists open sets $U_C, U_D$ where $C \subset U_C, D \subset U_D$ and $U_C \cap U_D = \emptyset$ . That is, a space is normal if disjoint closed sets can be separated by disjoint open sets.

Proof: let $x \in C$ then by regularity, there exists $\epsilon_x > 0$ such that $B_x(\epsilon_x) \cap D = \emptyset$ . Similarly for each $y \in D$ there exists $\epsilon_y > 0$ such that $B_y(\epsilon_y) \cap C = \emptyset$ .

Now let $U_C = \cup_{x \in C} B_x(\frac{\epsilon_x}{3})$ and $U_D = \cup_{y \in D} B_y(\frac{\epsilon_y}{3})$ . Both $U_C, U_D$ are open and contain $C, D$ respectively. We must show that $U_C \cap U_D = \emptyset$ .

If $z \in U_C \cap U_D$ there exists $x \in C, y \in D$ where $d(x,z) \leq \frac{\epsilon_x}{3}$ and $d(y,z) \leq \frac{\epsilon_y}{3}$ . Therefore by the triangle inequality, $d(x,y) \leq \frac{\epsilon_x}{3} + \frac{\epsilon_y}{3} < 2max(\frac{\epsilon_x}{3}, \frac{\epsilon_y}{3})$ which is impossible because $\epsilon_x, \epsilon_y$ were chosen so as to be less than the distance from $x$ to $D$ and $y$ to $C$ respectively.

Note: not all regular spaces are normal!

metric spaces, Separation Axioms normal, regular, separation axioms, T3, T4

Some study questions (in no particular order)

Leave a comment Posted by collegemathteaching on March 5, 2015

1. Let $U \subset R^2$ . Declare $U$ to be open in topology $\mathscr{T}_r$ if the following holds: given $(x,y) \in U$ and radian angle $\theta \in [0, 2 \pi)$ there exists $\delta_{\theta} > 0$ such that the open line segment $r(t) = \langle x,y \rangle + t \langle cos(\theta), sin(\theta) \rangle \delta_{\theta}, t \in [0,1)$ is also in $U$ . That is, for all $(x,y)$ is $U$ there is, for every direction, some open segment starting at $(x,y)$ that stays in $U$ . This topology is described in Willard in problem 3A, part 4 (“radially open”).

Is this topology finer, coarser or incomparable to the usual topology of the plane?

(hint: consider $(0,0)$ and consider the set (described in polar coordinates): $r < e^{-\frac{1}{2 \pi -\theta}}, \theta \in [0, 2 \pi)$ : is this set open in the radial topology? Is it open in the usual topology?

2. Let $A \subset R^1$ in the usual topology. Assume that $A$ is non-empty. Let $a = lub\{x \in A \}$ . If $A$ is closed, is it always true that $a \in A$ ? If $A$ is open, is it always true (or EVER true) that $a \in A$ ?

3. Same questions as 2, but now assume that $R$ has the “lower limit” topology (open sets are generated by $[c,b), b > c$ ).

4. Let $f:(X, \mathscr{T}_1) \rightarrow (Y, \mathscr{T}_2)$ be a continuous, onto function between Hausdorff topological spaces. Endow $X \times Y$ with the product topology. Prove (or provide a counter example): $\Gamma = \{(x,y), | x \in X, y = f(x) \}$ is a closed set in $X \times Y$ .

5. Given $R^Z$ (countable product of the real line), describe a set that is open in the box topology that is not open in the product topology.

6. Given $f: X \rightarrow Y$ is continuous and $C \subset Y$ is closed, prove that $f^{-1}(C)$ is closed in $X$ .

If $X$ is a topological space and $a_n$ is a sequence of points in $X$ , we say that $l \in X$ is a limit point for the sequence if, for every open set $U, l \in U$ , there exists at least one $a_n \neq l$ where $a_n \in U$ . We say that the sequence converges to $a$ if, for every open set $U, a \in U$ , there is some number $M$ such that, for all $n \geq M, a_n \in U$ .

7. Suppose that $f: X \rightarrow Y$ is continuous. Then if $x_n \rightarrow x, f(x_n) \rightarrow f(x)$ .

8-11. Let $a_n = \frac{1}{n}, b_n = \frac{n}{n+1}, c_n = (-1)^n b_n$

8. For each sequence $a_n, b_n, c_n$ , find the limit points and if the sequence converges if $R$ has the usual topology.

9. For each sequence $a_n, b_n, c_n$ , find the limit points and if the sequence converges if $R$ has the lower limit topology.

10. For each sequence $a_n, b_n, c_n$ , find the limit points and if the sequence converges if $R$ has the discrete topology.

11. For each sequence $a_n, b_n, c_n$ , find the limit points and if the sequence converges if $R$ has the finite complement topology.

12. Show that a sequence can have at most ONE limit point if $X$ is Hausdorff (has the $T_2$ property). Show that this is false if the topology is not assumed to be Hausdorff.

13. Let $X$ be a Hausdorff topological space. Show that a one point set is a closed set. Is this true of the space is merely $T_1$ ?

14. Let $Y$ be a Hausdorff topological space. Let $f:X \rightarrow Y$ and $g:X \rightarrow Y$ be continuous functions. Show: if $S = \{ x| f(x)=g(x) \}$ is a closed set.

15. Show that the comb spaces and the topologist’s sine curve are connected sets (in the usual subspace topology of $R^2$ ).

16. Show that $R$ with the usual topology, the lower limit topology, the discrete topology and the finite complement topology are NOT topologically equivalent spaces.

17. Show that the unit circle (usual subspace topology) and the unit interval are not topologically equivalent spaces.

18. Show that the “closed unit interval” is not a connected set in the lower limit topology.

19. Show that the following set $\{ (x,y), y = x \sin(\frac{1}{x}, x \in (0, \pi] \} \cup \{(0,0) \}$ is both a connected set and a path connected set (usual subspace topology).

20. Let $X$ have topologies $\mathscr{T}_a, \mathscr{T}_b$ . Suppose $\mathscr{T}_a \subset \mathscr{T}_b$ (that is the topology $\mathscr{T}_b$ is finer than the topology $\mathscr{T}_a$ . Show that if $(X, \mathscr{T}_a )$ is Hausdorff, then so is $(X, \mathscr{T}_b)$ . Does it work the other way? Why or why not?

21. Consider the following “sequence of sequences” in $R^{Z}$ : $x_1 = (1, 0, 0, ...), x_2 = (0, \frac{1}{2}, 0, 0, 0,..), x_3 = (0, 0, \frac{1}{3}, 0, 0,...)$ , $x_n$ is the point that is $\frac{1}{n}$ in the n’th coordinate, and 0 in the other coordinates. That is, $\pi_k (x_n) = \frac{1}{k}$ if $k=n$ and zero otherwise.

Does $x_n$ converge to $(0, 0, 0,.....0, )$ in the product topology? What about in the box topology?

22. Suppose $A \subset X$ is closed. Show that $Fr(A) \subset A$ .

23. Suppose that for all $i \in \{1, 2, 3, ...\}$ we have that $X_i$ is a Hausdorff topological space (note: the $X_i$ might not be topologically equivalent spaces).

Show: $\Pi^{\infty}_{i}X_i$ is Hausdorff in the product topology. Is this true if we use the box topology?

24. Show that if $A, B$ are connected subsets of $X$ and $A \cap B \neq \emptyset$ then $A \cup B$ is connected.

25. Show that if $A$ is a connected set, then so is $\bar{A}$ . If $\bar{A}$ is connected, does it follow that $A$ is connected?

26. Show that if $X, Y$ are connected topological spaces, then so is $X \times Y$ .

27. Show that if there exists a non-empty subset $A \subset X$ where $A \neq X$ and $A$ is both open and closed, then $X$ is NOT a connected space.

28. Let $A_n$ denote a set with precisely $n$ elements. For $n \in {2, 3, 4, 5, 6}$ , find all possible topologies for $A_n$ .

29-30: A topological space $X$ is called “topologically homogeneous” if, given any two points $x, y \in X$ , there is a homeomorphism $h: X \rightarrow X$ where $h(x) = y$ .

29. Are the following topological spaces (usual topology) topologically homogeneous: $[0,1] \subset R$ , $(0,1) \subset R$ , $S^1 \subset R^2$ , “the wedge of 2 circles (last homework)” ?

30. Prove that $R^n$ (usual topology, $n$ finite) is topologically homogeneous.

connected sets, continuous functions, metric spaces, open set, path connected, Separation Axioms, sequence, subspace topology, topologies study problems

Box versus Product Topology

Leave a comment Posted by collegemathteaching on March 5, 2015

Since the product and box topologies only differ on spaces that are infinite products (they are the same on spaces that are finite products), we will demonstrate these concepts on $R^Z$ (the countable product of real numbers, which is the same as the set of all real number sequences).

Remember that the product topology is the coarsest topology that makes each projection function $\pi_k$ continuous.

Now lets look at $\pi_1^{-1}(a,b) = (a,b) \times R \times R \times R \times R .....$

Now look at $\pi_2^{-1} (c, d) = R \times (c,d) \times R \times R.....$

Also, $\pi_3^{-1} (r,s) = R \times R \times (r,s) \times R \times R ...$

We see that the inverse image of an open interval of the $k'th$ projection function is just the product of an infinite number of copies of the real line with the exception of the k’th slot, which sees that open interval as the factor.

Such sets for the basis for the product topology.

Now if we look at the FINITE intersection of such sets, we obtain sets which are the product of the real line, with the exception of a FINITE number of factors, which are copies of the various intervals.

Hence the product topology consists of $\Pi^{\infty}_{i=1} U_i$ where $U_i = R$ for at most FINITELY MANY $i$ ; for these $U_i$ is open in $R$ (here we use the usual topology).

What about the box topology?
In the box topology, the open sets are $\Pi^{\infty}_{i=1} U_i$ where $U_i$ is open in $R$ .

As we discussed in class, there are just too many open sets in the box topology for this topology to be useful.

Let’s look at some examples to see if you are getting it.

I’ll list some sets in $R^{Z}$ and you tell me whether such sets are open in the box topology, open in the product topology, or open in neither topology.

1. $U = \Pi^{\infty}_{i=1} U_i$ where $U_i = R$ if $i$ is odd, and $U_i = (i, i+1)$ if $i$ is even.

2. $U = \Pi^{\infty}_{i=1} U_i$ where $U_i = R$ if $i \notin \{1, 4, 7, 33 \}, U_1 = (0,2), U_4 = (0, \infty), U_7 = (-1, -\frac{1}{2}), U_{33} = (-\infty, 13)$

3. $U = \Pi^{\infty}_{i=1} U_i$ where $U_i = R$ if $i \neq 17$ and $U_{17} = [1, 3]$ .

4. $U = \Pi^{\infty}_{i=1} U_i$ where $U_i = R$ if $i > 100$ and $U_i = (-\frac{1}{i}, \frac{1}{i})$ if $i \leq 100$ .

5. $U = \Pi^{\infty}_{k=1} U_k$ where $U_k = (-\frac{1}{k}, \frac{1}{k})$ for all $k$ .

topologies box topology, product topology

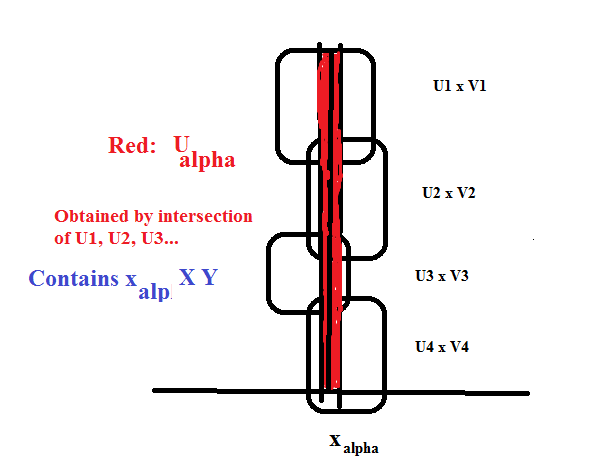
Products of topological spaces

Leave a comment Posted by oldgote on March 3, 2015

For this course we will mostly work with either finite or countable products of spaces, though we’ll take just a glance at one example of an uncountable product of spaces.

We know what the Cartesian product of a set of spaces is: given a collection of sets $X_{\alpha}, \alpha \in I, \Pi X_{\alpha}$ consists of the set of all maps $f: I \rightarrow \cup X_{\alpha}$ where $f(\alpha) \in X_{\alpha}$ . Often we don’t think of it this way but rather think of the elements $\Pi X_{\alpha}$ consisting of sequences of elements $x_{\alpha} \in X_{\alpha}$ ; these sequences can be thought of as “tuples” if the index set is finite.

So, the issue is: how do we endow this product with a topology? There are two basic ways (as well as a few esoteric ways); these basic ways are equivalent of we are talking about a finite product.

First, we assume that there is a given topology to each factor space $X_{\alpha}$ . We also have a “projection function” $\pi_{\beta}: \Pi X_{\alpha} \rightarrow X_{\beta}$ where $\pi_{\beta} (x_1, x_2, ...x_{\beta}, ...) = x_{\beta}$

The Product Topology (aka Tychonoff Topology).

The open sets are generated by $\Pi U_{\alpha}$ where each $U_{\alpha}$ is an open set in $X_{\alpha}$ and, for all but a finite number of $\alpha , U_{\alpha} = X_{\alpha}$

Note: this is the topology you would have guessed if we were putting it on a FINITE product of topological spaces, as in this case, the open sets in the product come from a finite product of open sets from the respective factor spaces.

If we drop the “all but a finite number” of the $U_{\alpha}$ have to be $X_{\alpha}$ we then have the box topology. The box topology is rarely used.

To see why: imagine the set of real sequences and suppose we wanted to try to get a sequence of sequences to converge to the sequence of all zeros (that is, converge at every “slot”). Now consider the sequence of sequences $x_k = \Pi \{\frac{1}{k} \}$ which certainly converges to the sequence of all 0’s point wise (that is, converges to the sequence of all 0’s in the product topology) does NOT converge to the sequence of all zeros in the box topology. Here is why: $U = \Pi_{n} (-\frac{1}{n^n}, \frac{1}{n^n} )$ is open in the box topology. So if we go far enough out on $x_k$ to find $\frac{1}{k} < \frac{1}{n^n}$ if we go out far enough out on the factor spaces, we’ll find $m$ large enough that $\frac{1}{k} > \frac{1}{m^m}$ hence no $x_k$ can lie in $U$ . Remember that the factor intervals shrink to an arbitrarily small size if you go out far enough in the factors.

Here is an illustration:

$x_1 = (1, 1, 1, 1, 1, 1, ...)$
$x_2 = (\frac{1}{2}, \frac{1}{2}, ......\frac{1}{2},.....)$

$x_n = (\frac{1}{n}, \frac{1}{n}, .....\frac{1}{n}, ....)$

In any reasonable topology, we should have $x_n \rightarrow (0, 0, 0, ....)$

But in the box topology,

$(-1,1) \times (-\frac{1}{4}, \frac{1}{4}) \times (-\frac{1}{27}, \frac{1}{27}) \times (-\frac{1}{256}, \frac{1}{256}) ....\times (-\frac{1}{n^n}, \frac{1}{n^n}) \times....$ is an open set which contains $(0, 0, ...0,...)$ but contains no element of $x_n$ as the factor intervals shrink to an arbitrarily small size.

So the box topology makes convergence too difficult and is therefore not used much.

More on the product topology: the product topology is the coarsest topology for which each projection function is continuous; after all for each open $U \subset X_{\alpha}$ we need each $\pi_{\alpha}^{-1}(U)$ to be open in $\Pi_{\beta} X_{\beta}$

Note: the product topology is sometimes called the “topology of pointwise convergence”.

I’ll explain: let $f_1, f_2, f_3....$ be a sequence of functions of the real line to the real line. We say that $f_n \rightarrow f$ pointwise if, for all $x$ and all $\epsilon >0$ there exists $M > 0$ such that, for all $n > M, |f_n(x) -f(x) | < \epsilon$ . That is $|f_n(x) - f(x)| \in \pi^{-1}_{x} ((- \epsilon, \epsilon))$ which is an open set in the product topology where the product is taken over all $x$ (uncountable product).

functions, sequence, topologies box topology, product topology

← Older posts

	anon31245 on Some questions
	anon31245 on Some questions
	Cantor Sets/Spaces P… on Cantor Set: Part I
	Cantor Set: Part I \|… on Special result: perfect compac…
	Connected Sets in th… on Least Upper Bound Postulate fo…